A palavra Estatística surge apenas no século XVIII e deriva do latin Statu, que significa estado. Nessa altura a estatística consistia numa série de estudos, encomendados pelo estado (quem governava um determinado país), sobre os números relativos à população e os seus bens (exemplo: nascimentos, mortes, idades, etc.…).
Nos nossos dias, a estatística desenvolveu-se e é considerada uma ciência fundamental para efectuar estudos sobre saúde, economia, educação, ambiente, etc…
"Ciência que dispõe de processos apropriados para recolher, organizar, classificar, apresentar e interpretar conjuntos de dados"
O objectivo desta ciência é:
- descrever e compreender melhor as situações em estudo;
- tomar decisões mais acertadas;
- fazer previsões;
- planear adequadamente ações futuras.
Instrumentos da Estatística
Inicialmente é necessário organizar os dados provenientes dos questionários/inquéritos feitos.
Equipas de futebol preferidas dos alunos da turma 5º D
Benfica Benfica Porto Sporting Sporting
Benfica Sporting Benfica Benfica Benfica
Sporting Benfica Porto Benfica Benfica
Sporting Benfica Benfica Benfica Sporting
Equipas Frequência absoluta*
S. L. B. - 12
F. C. P. - 2
S. C. P. - 6
Total 2
*- É o número de vezes que uma situação se repete.
Os gráficos são formas simples e eficientes de apresentar e transmitir as situações estudadas.
Gráficos de barras
Para construir os gráficos de barras é necessário que:
- as barras, devem ter a mesma largura e a altura depende da frequência absoluta.
- o gráfico tenha um título informativo sobre o assunto a que se refere o gráfico.
- nos dois eixos ou retas devem colocar-se o assunto, no eixo horizontal e no eixo vertical coloca-se a frequência absoluta.
- as barras devem estar separadas por espaços iguais (quando existem).
Pictogramas
Neste caso, a unidade gráfica é uma figura alusiva ao tema em estudo e repete-se tantas vezes quantas as necessárias para representar cada uma das frequências.
Gráficos circulares
Num gráfico circular as amplitudes dos diferentes setores são proporcionais às frequências que representam.
Média aritmética
A média ajuda a perceber uma situação, pois apresenta um valor aproximado da maioria dos resultados.
Para a calcular devemos ter os valores não muito dispersos. Primeiro somam-se todos os valores e depois divide-se esse valor pelos valores considerados.
Para a situação anterior não é possível calcular a média pois não existem dados com valores. Mas se tiveres as idades dos alunos da turma 5º D já é possível.
Imagina que tens as seguintes idades:
10, 12, 10, 10, 10 ,11, 10, 10, 11, 12, 13, 10, 11, 10, 11, 10, 11, 10, 12, 10
Para a calcular a média deves:
Média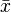= (10+12+10+10+10+11+10+10+11+12+13+10+11+11+10+10+11+10+12+10)/20=214/20=10,7
Isto quer dizer que em média os valores rondam os 11 anos.
Moda
A Moda de um conjunto de resultados é aquele que aparece mais vezes, isto é, com mais frequência.
No caso das preferências clubísticas do 5º D verifica-se que o resultado mais frequente é o Benfica, logo é a Moda destes resultados.
No caso anterior, a das idades dos alunos da mesma turma, a idade mais frequente é 10 anos, logo é a moda.
Pode acontecer existir uma moda, duas modas ou não haver moda.
Probabilidade de um acontecimento
Uma previsão é uma indicação do que poderá acontecer no futuro, feita com base em resultados já conhecidos.
Faz a seguinte experiência, Pega num pionés e lança-o ao ar de moda que caia sobre a tua mesa de trabalho. Espera que ele pare e verifica como ficou. De bico para cima, de bico para baixo ou de lado. Faz isso 30 vezes seguidas.
Fazes uma tabela de frequências para verificares a situação.
Estado do pionés Contagem Frequência Absoluta
Bico para cima
Bico para baixo
De lado
Total 30
Depois de preencheres a tabela, compara o teu trabalho com o de outra pessoa que faça esta experiência.
Depois podes fazer questões sobre isso:
- Qual o resultado mais frequente?
- E o menos frequente?
- Há algum acontecimento impossível? Porquê?
- Que acontecimento(s) pode(m) ser provável(eis)?
Esta experiência também pode ser feita usando bolas ou dados.
Exercícios:
- http://sites.google.com/site/mariaodetecosta/Estatstica.htm
- http://www.ajudaalunos.com/matematica/fichas/FichaGraficos.doc
- http://www.ajudaalunos.com/matematica/fichas/Fichatra6estatistica.doc
- http://www.ajudaalunos.com/Quiz_mat/estatis5_html/indice_estatistica.htm
- http://www.ajudaalunos.com/Quiz_mat/media6_html/indice.htm
Apresentações:
0 comentários:
Enviar um comentário