Os círculos são figuras geométricas que se designam por "discos". O círculo é o conjunto de pontos localizados dentro de uma circunferência.
A circunferência é a linha que limita o círculo, ou seja, é o conjunto de todos os pontos que se encontram à mesma distância de um ponto central (designado por centro da circunferência).
Na imagem anterior a circunferência está a representada a vermelho e o círculo a verde.
Podes observar outros elementos:
- a corda, que é um segmento de recta que une dois pontos da circunferência.
- o diâmetro, que é uma corda, mas é especial pois passa pelo centro da circunferência, o ponto O.
- o raio, que é um segmento de recta que une o centro e um ponto qualquer da circunferência.
Deve ter-se em conta que o diâmetro (d) é o dobro do raio (r).
Relações entre ângulos, retas e polígonos
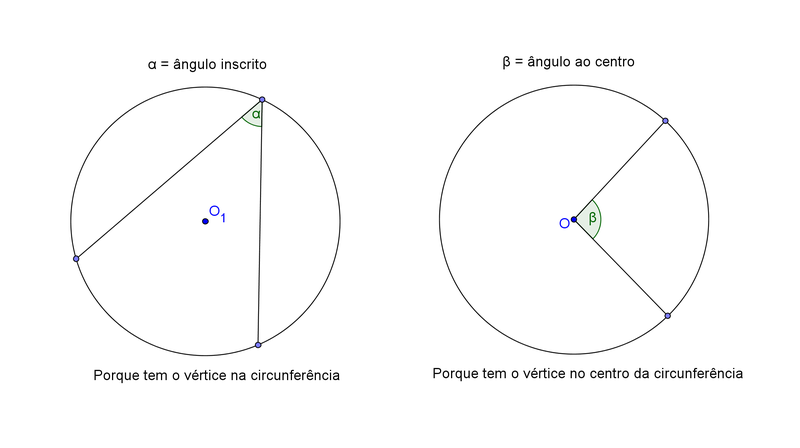
- Numa circunferência podemos ter um ângulo cujo vértice seja o centro da circunferência. A este ângulo chama-se ângulo ao centro. Podemos ter por outro lado um ângulo inscrito na circunferência cujo vértice fica num dos pontos da circunferência.
- Num círculo podemos observar um setor circular, que é uma interseção de um ângulo ao centro com o círculo.
- Na próxima figura podemos observar vários polígonos inscritos numa circunferência, pois os seus vértices são pontos da circunferência.
- A próxima reta s é tangente à circunferência, pois passa por um ponto pertencente à circunferência. Essa reta é perpendicular ao raio apresentado.
- De seguida, podes observar polígonos circunscritos a uma circunferência, pois os seus lados são tangentes à circunferência.
- Num polígono regular inscrito numa circunferência, os segmentos que unem o centro da circunferência aos pés das perpendiculares tiradas do centro para os lados do polígono são todos iguais e designam-se por apótemas.




.jpg)
.jpg)
.jpg)
.jpg)
Muito bom este site .....
ResponderEliminarsuper bom
ResponderEliminar