Ângulos

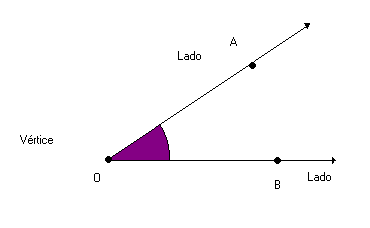
O ângulo é uma região do plano composta pela abertura de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo. A abertura do ângulo é medida em graus, a que damos o nome de amplitude.

Num polígono qualquer, como os que podes ver mais abaixo, podemos ter dois tipos de ângulo, os internos a verde e os externos a vermelho.

Applet em geogebra -ângulos internos e externos de um triângulo
Clica aqui no link

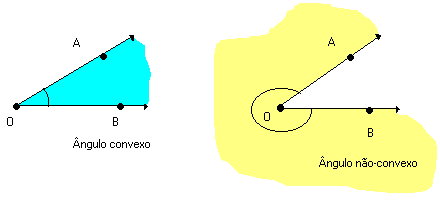
Podes ainda ter ângulos convexos (se têm mais de 180º) e côncavos( se têm menos de 180º).

Tipos de ângulos




De acordo com a amplitude de cada ângulo podemos classificá-lo como:

- Ângulo agudo- Ângulo cuja amplitude é maior do que 0° e menor do que 90°.

        

- Ângulo reto- tem uma amplitude de 90º.

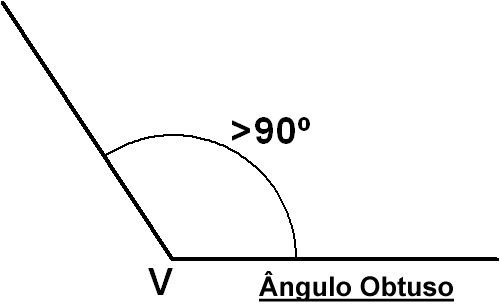
- Ângulo obtuso- tem amplitude compreendida entre 90º e 180º.

- Ângulo raso- tem de amplitude 180º.

- Ângulo giro- tem de amplitude 360º.

Medir um ângulo com a ajuda de um transferidor

Um transferidor

Clica no próximo site para descobrires a amplitude de uma ângulo.

http://www.amblesideprimary.com/ambleweb/mentalmaths/protractor.html

Relações entre ângulos

- 2 ângulos são geometricamente iguais se tiverem a mesma amplitude.

- 2 ângulos são adjacentes se têm um lado comum.

Applet em geogebra - ângulos adjacentes

- Dois ângulos são suplementares quando a respetiva soma for igual a um ângulo raso.

- Dois ângulos são complementares quando a respetiva soma for igual a um ângulo reto.

- Dois ângulos são verticalmente opostos quando têm o mesmo vértice e os lados de um estão no prolongamento dos lados do outro. (estão com mesma cor)

Ex.: ∢AVB e ∢DVC são verticalmente opostos.

Dois ângulos verticalmente opostos têm a mesma amplitude: a = b

Duas retas concorrentes, que se cruzam num ponto comum, formam dois pares de ângulos verticalmente opostos: a = b e c = d.

Applet em geogebra - ângulos verticalmente opostos

- Num sistema de duas retas paralelas cortadas por uma terceira, chamada secante, chamam-se ângulos alternos-externos aos pares a, c e b, d assinalados na figura.

Os ângulos alternos-externos são geometricamente iguais, por isso têm a mesma amplitude; a amplitude de a é igual à de c, o mesmo sucedendo entre b e d.

- Num sistema de duas retas paralelas cortadas por uma terceira chamam-se ângulos alternos-internos aos pares e, g e f, h assinalados na figura.

Os ângulos alternos-internos são geometricamente iguais, por isso têm a mesma amplitude; a amplitude de e é igual à de g, o mesmo sucedendo entre f e h.

Por isso, concluímos que os Ângulos alternos externos são geometricamente iguais e os os Ângulos alternos internos também são geometricamente iguais.

- A soma das amplitudes dos ângulos externos de um qualquer triângulo é 360º.

Applet em geogebra ( clica no link)

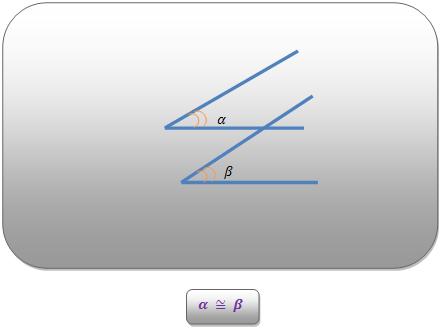
- 2 ângulos têm lados diretamente paralelos logo são considerados congruentes ou suplementares.

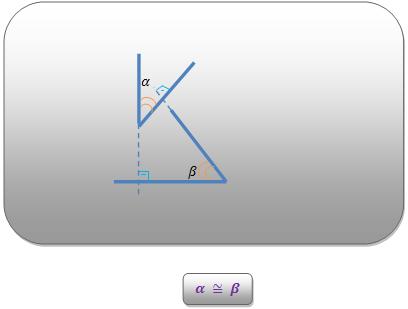
- 2 ângulos têm lados diretamente perpendiculares logo são considerados congruentes ou suplementares. 

- Podes observar ângulos inscritos numa circunferência na próxima animação: http://clubes.obmep.org.br/blog/applet-angulo-central-e-angulo-inscrito/

No próximo link podes encontrar um applet onde podes observar muitas das relações de que falámos.
http://egeom.blogspot.pt/p/geometria-plana-applet.html

- Para construir um ângulo igual à soma de dois ângulos dados segue os seguintes passos:

1- Traçar arcos de circunferência, no dois ângulos, com a mesma abertura.
2- Traça um dos lados do ângulo, por exemplo GH.
3- Colocar em H o compasso coma abertura igual ao comprimento de BC e traça um arco de circunferência. Encontras um ponto de interseção , ponto I.
4- Coloca em I o compasso com abertura igual ao comprimento de EF e traça um arco de circunferência. Encontras o ponto J.
5- O ângulo HGJ é a soma dos dois anteriores.

- Conversão de medidas de amplitude. O grau divide-se em duas subunidades, o minuto e o segundo.

ex. 5º46' - quantos minutos?

1º = 60' logo 5º = 5 x 60' = 300'
300' + 46' = 346' 

R: 346 minutos do grau

ex. 23716'' - quantos graus, minutos e segundos?

23716'' : 60'' = 395'  resto 16''

Como  60'' = 1' , vamos ver quantos minutos tem 23716 segundos.

São 395 minutos e 16 segundos

395' : 60' = 6º  resto 35'

Como 60' = 1' , vamos ver agora quantos graus têm 395 minutos.

R: São 6º35'16''

. Adição de medidas de amplitudes de ângulos

ex. 16º18'32'' + 7º55'30'' = 23º73'62''  mas como o minuto e o segundo só podem atingir os 60, temos de reduzir 73' em graus e minutos e o 62'' em minutos e segundos.

73' = 1º13' e 62''=1'2''

R: 24º14'2''

. Subtração de medidas de amplitudes de ângulos

ex. 28º3'24'' - 8º15'30''

Não podemos subtrair o subtrativo pois os minutos e os segundos são superiores aos do aditivo. Assim temos que transformar o primeiro para aumentar o valor dos minutos e segundos.
Tiramos ao 28º um grau e fica 27º. 
Adicionamos 60 minutos que equivale ao grau que tirámos.
Já temos 27º63'24''.
Agora para alterar os segundos tiramos um minuto e passámo-lo para segundos, ou seja, adicionar 60 segundos.
Fica 27º62'84''

Agora já podemos fazer a subtração. 

R: 19º47'54''

Como construir a bissetriz de um ângulo?

A bissetriz do ângulo é uma semirreta contida no ângulo, de origem no vértice e que forma com cada um dos lados ângulos iguais. Vê o próximo vídeo para aprenderes a construir a bissetriz.

angulos_revisões_7