Como podes fazê-lo?
Se tens uma chávena de farinha vais necessitar do dobro, ou seja duas, pois 8 (pessoas) é o dobro de 4 (pessoas)!
Na receita precisas de litro e meio de leite, logo passas a necessitar do dobro, ou seja, 3 litros de leite!
E assim sucessivamente…
Se reparares basta multiplicar por dois, ou fazeres o dobro de, para cada uma das quantidades.
E se a receita fosse para seis pessoas???
Tens que ver que relação há entre 6 e 4. Para obter o seis deves multiplicar o 4 por um e meio.
Logo para obter cada um dos ingredientes deves multiplicar por 1,5 cada uma das quantidades.
Elaboramos uma grelha com os cálculos que fizemos para o leite, para um bolo para 4 pessoas, 6 pessoas, 8 pessoas e 12 pessoas.
Número de pessoas
4 - 1 litro
6 - 1,5 litros
8 - 2 litros
12 - 3 litros
Se dividires
4 : 1 = 4;
6 : 1,5 = 4;
8 : 2 = 4;
12 : 3 = 4
Obténs sempre o mesmo valor.
Duas grandezas são diretamente proporcionais quando é constante (é o mesmo) o quociente entre cada valor de uma grandeza e o correspondente valor da outra grandeza.
Ao quociente constante dá-se o nome de constante de proporcionalidade.
No caso anterior a constante de proporcionalidade é 4.
Quando efetuaste aquelas divisões, podias tê-las transformado em frações.
Cada uma dessas frações designa-se por razão. Ver o exemplo mais abaixo.
Os números presentes numa razão/quociente chamam-se termos. No primeiro caso o 4 é o antecedente e o 1 é o consequente. No segundo caso, o antecedente é o 8 e o consequente é o 2.
Podes escrever assim:
Diz-se que 4 está para 1 assim como 8 está para 2.
A esta igualdade chamamos proporção entre duas razões ou quocientes.
Cada um dos números ali presentes tem uma designação.
O 4 é o 1º termo, o 1 é o 2º termo, o 8 é o 3º termo e o 2 é o 4º termo.
Os números que estão a vermelho chamam-se meios e os que estão a verdes chamam-se extremos.
- http://www.rpedu.pintoricardo.com/Fichas_interactivas/Razao_proporcao/razao_proporcao.htm
Se observares bem consegues perceber que se multiplicares os extremos dá-te 8 e se multiplicares os meios também te dá 8.
4 x 2 = 8 x 1 = 8
Esta é a propriedade fundamental das proporções que te diz que o produto dos meios é igual ao produto dos extremos.
Será que quando comparas a idade e o peso de uma pessoa são grandezas directamente proporcionais?
Verifica o quadro seguinte:
Idade: Peso
1 anos - 10 kg
2 anos - 12 kg
3 anos - 14,5 kg
4 anos - 16 kg
Verificando se a constante e a mesma...
1 : 10 = 0,1
2 : 12 = 0,17
3 : 14,5 = 0,20
4 : 16 = 0,25
Como os quocientes são diferentes então não existe proporcionalidade entre as duas grandezas, a idade e o peso.
Vamos utilizar a propriedade fundamental das proporções para resolver o problema seguinte.
O João foi à loja dos animais comprar peixes.
Quando lá chegou viu uma tabela:
Número de peixes Custo (euros)
2 4
8 16
5 10
Para verificar se há proporcionalidade directa basta efectuar os quocientes/razões. Verificas que:
Há uma constante de proporcionalidade que é 0,5.
Se o João quiser comprar 4 peixes quanto vai ter que gastar?
O x é o valor que queres saber!
Como o podes descobrir?
Recorda a propriedade fundamental das proporções…
4 x 4 = 2 x X
16 = 2 x X
X = 16 : 2 = 8 euros
Assim multiplicas 4 pelo 4 e depois divides o resultado por 2!!! A esta regra chama-se regra de três simples!!
Já ouviste falar em percentagem (%), na TV, na escola, nos jornais, revistas, etc…
Mas sabes o que isto representa?
Quando tens as notas dos testes, normalmente são dadas em percentagem.
Se tiveres 65% num teste será que tens positiva ou negativa??
Isto quer dizer que se tivesses o teste todo certo terias 100%. Logo tiveste 65 pontos em 100 pontos. Tiveste mais de metade, certo?
Tiveste nota positiva!!
E se tivesses… 40%? Aí já terias menos de metade de 100, logo era uma nota negativa.
Assim percentagem é uma razão onde o consequente/denominador é sempre o 100. (É qualquer coisa em 100)
a) Na tua escola há 18% de alunos que se inscreveram no clube da rádio. Sabendo que os alunos são 450, quantos foram os alunos inscritos?
O total de alunos, 450, equivale aos 100.
Já sabes como resolver este problema:
Podes fazê-lo de outra forma:
18% de 450… 0,18 x 450 = 81 alunos
b) Num saco tens smarties, 3 vermelhos, 4 amarelos e 5 verdes. Qual é a percentagem de smarties amarelos?
Tens de indicar a fração de smarties amarelos e transformar a fração em numeral decimal.
Se transformar depois o numeral decimal numa fração decimal, cujo denominador é o 100, o numerador corresponde à percentagem que queremos obter.
33%
c) A turma da Joana recebeu os teste de Ciências. A professora disse aos alunos que as questões do teste tinham a mesma cotação. Sabendo que a Joana teve 12 questões corretas, em 22 questões calcula o valor da percentagem que obteve no teste.
Podes resolver a questão de duas formas:
1-
2-
d) Nos gráficos também podes observar percentagens.
Consegues dizer quantos familiares têm Peugeot?
Metade das pessoas escolheu esse carro. Se são 600 alunos, quer dizer que metade são 300 familiares.
E quantos têm Opel?
25% de 600 0,25 x 600 = 150 pessoas
. http://www.rpedu.pintoricardo.com/Fichas_interactivas/quiz_ex3.html
. http://www.rpedu.pintoricardo.com/Fichas_interactivas/quiz_ex3.html
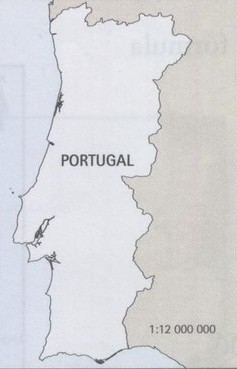
Junto à figura está indicada a escala usada
1: 12000000 ou 1/12000000
Quer dizer que 1 cm no mapa corresponde a 12.000.000 cm na realidade.
Quando a escala é maior que 1 temos uma imagem ampliada.
Quando a escala é menor que 1 temos uma imagem reduzida.
Exercícios:
- http://www.ajudaalunos.com/matematica/fichas/fichapropor1.pdf
- http://www.ajudaalunos.com/matematica/fichas/fichaproporcionalidade.pdf
- http://sites.google.com/site/mariaodetecosta/Proporcionalidade.htm
- http://www.ajudaalunos.com/Quiz1/proporcidirectaestatis5.htm
- http://matematica6.no.sapo.pt/Ficha_trabalho_Proporcionalidade.htm
- http://matematica6.no.sapo.pt/Escalas_Revisao.htm
- http://www.ajudaalunos.com/Quiz_mat/proporc_html/indice_propor_cao.htm
- http://www.ajudaalunos.com/Quiz_mat/percent_html/indice_percent.htm
- http://aesap.edu.pt/moodle/mod/hotpot/view.php?id=434
Apresentações:
http://www.slideshare.net/raquelrico/razes-e-propores
http://www.slideshare.net/tetsu/regrade3simples




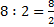
















Sem comentários:
Enviar um comentário