Hoje vamos aprender um pouco mais sobre o cilindro de revolução.
Como sabes o cilindro é um sólido geométrico.
Uma lata de spray, um tubo de cola, uma lata de ervilhas, são exemplos de objectos de forma cilíndrica.
O cilindro de revolução é limitado por:
- duas faces planas, que são círculos e que representam as bases do cilindro;
- uma superfície curva, à qual se chama superfície lateral.
As bases do cilindro estão situadas em planos paralelos.
Como tem uma face que é curva encontra-se no grupo dos não poliedros, como é o caso da esfera e do cone!
O cilindro de revolução que podemos ver na figura foi gerado pelo retângulo [ABCD] , quando este roda uma volta completa em torno do lado [AB] .
Ao lado [AB] chamamos eixo do cilindro de revolução, e ao seu comprimento chamamos altura do cilindro de revolução. A geratriz do cilindro é o lado [CD], pois este gera a superfície lateral do cilindro. Os lados [AD] e [BC] que geram as bases do cilindro são raios.
A altura dum cilindro de revolução é igual ao comprimento das geratrizes.
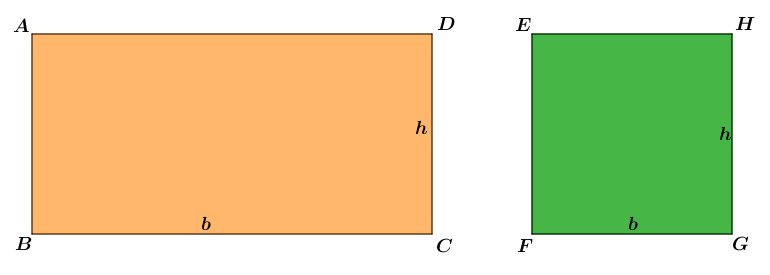
Como podes ver, as figuras geométricas que fazem parte da planificação do cilindro, são um retângulo e dois círculos.
Perímetro da base do cilindro
Já aprendeste que as figuras geométricas tem uma linha que as limita.
Podemos calcular o seu comprimento calculando o perímetro de cada uma.
Já o fizeste para as figuras cujos lados tem segmentos retos.
Para figuras como o círculo ainda não o fizeste.
Vamos então descobrir como se faz isso. Podes pegar num círculo em papel e com uma corda descobrir o comprimento da circunferência. Compara o valor que te deu com o seu diâmetro.
Verificaste que o perímetro é um pouco mais que o triplo do diâmetro.
Os matemáticos tentaram saber se existia um número que pudessemos multiplicar pelo diâmetro para descobir qual o diâmetro.
Pois é... e não é que conseguiram!!!
Descobriram um número com imensas casas decimais, que chamaram Pi:
Assim verificaram que multiplicando o diâmetro (ou duas vezes o raio) do círculo por esse Pi (3,14 aproximadamente) obtinham o perímetro do círculo.
Sobre isto aqui vai um poema!
O PERÍMETRO DO CÍRCULO
Com dois raios, eu já sei
um diâmetro posso obter
mas medir o comprimento
de uma circunferência
(o perímetro de um círculo)
é osso duro e difícil
que eu não consigo roer.
Ah se eu conseguisse
descobrir uma continha
muito fácil de fazer...
Media só o diâmetro
e depois lá calculava
o perímetro do círculo
sem nunca mais me perder.
Fui à lata de feijão
ao copo, ao frasco, à panela
medi tudo com cuidado
investiguei curiosa
com rigor e emoção
diâmetro, perímetro
perímetro, diâmetro
parecendo-me que em qualquer lado
devia estar bem guardado
o segredo, a solução.
E foi assim de repente
a olhar para tudo aquilo
que, subitamente, eu vi:
o triplo do diâmetro
(triplo mais um bocadinho)
permitia descobrir
o perímetro do círculo
sem precisar de o medir!
Três vírgula catorze e mais
um comboio infinito
de casinhas decimais
(que não vou utilizar).
Subitamente eu vi
e a professora contou-me
que aquele número estranho
mágico, misterioso
não era sequer perigoso
era só o número "pi"
E querem saber a melhor?
Dividam perímetro por pi
(por exemplo, no Equador)
e chegamos ao diâmetro
(por exemplo, o da Terra)
sem precisar de a cortar.
Porque Terra há só uma
e depois não se pode colar!
de Teresa Martinho Marques
Volume do cilindro
Para calcular o volume do cilindro basta multiplicar a área da base (área do círculo) e depois multiplicar pela altura do cilindro, ou seja a sua geratriz!
(nota: o h representa a altura e o ponto entre o pi e o raio ao quadrado é uma multiplicação)
Cilindro de Revolução by Maria Helena Cabrita Borralho on Scribd
Faz os seguintes exercícios sobre este assunto:http://www.ajudaalunos.com/matematica/fichas/FichadeTrab6cilindrocirculo.pdf
http://www.ajudaalunos.com/Quiz_mat/circulo_html/indice_circulo.htm



































.jpg)